Shaddy-Ethical-hacking: A C - PROGRAM TO FIND THE VALUE OF exp(0.5) USING TAYLOR SERIES

Sunday, 26 May 2013

0 A C - PROGRAM TO FIND THE VALUE OF exp(0.5) USING TAYLOR SERIES

TAYLOR SERIES

The Taylor series of a real or complex-valued function ƒ(x) that is infinitely differentiable in a neighborhood of a real or complex number a is the power series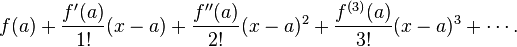

$f(a)+\frac {f'(a)}{1!} (x-a)+ \frac{f''(a)}{2!} (x-a)^2+\frac{f^{(3)}(a)}{3!}(x-a)^3+ \cdots.$

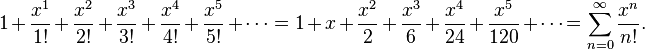
$1 + \frac{x^1}{1!} + \frac{x^2}{2!} + \frac{x^3}{3!} + \frac{x^4}{4!} + \frac{x^5}{5!}+ \cdots = 1 + x + \frac{x^2}{2} + \frac{x^3}{6} + \frac{x^4}{24} + \frac{x^5}{120} + \cdots\! = \sum_{n=0}^\infty \frac{x^n}{n!}.$

THE PROGRAM :

#include<stdio.h>
#include<math.h>
#include<float.h>
#include<conio.h>
void main()
{
    double x=0.5,e=1.0,term=1.0,fact=1.0;
    int i;
    for(i=1;term>=FLT_EPSILON;i++)
    {
        fact=fact*i;
        term=pow(x,i)/fact;
        e=e+term;
    }
    printf("\n Sum without using library function exp(%lf) = %lf \n",x,e);
    printf("\n Sum using library function exp(%lf) = %lf \n",x,exp(x));
    getch();
}

Just copy and paste into your Microsoft Visual C++ or Turbo C (these are program developing software)

Or else you can try this demo file and use it ...
Click HERE to download this file.
(Press ctrl+z and hit Enter to end the program)..
~NOTE~ : While executing if you get any warning then just ignore it and continue with your program...

IF FACE ANY PROBLEM DON'T FORGET TO COMMENT ...!!

Don't Forget to share....

Follow on Facebook : Ethical Hacking.